Triangulation#

Note

Based on (translated and slightly modified by ØF) notes from Hege B Fredriksen based on Fram Strait cruises (received 12.12.2024).

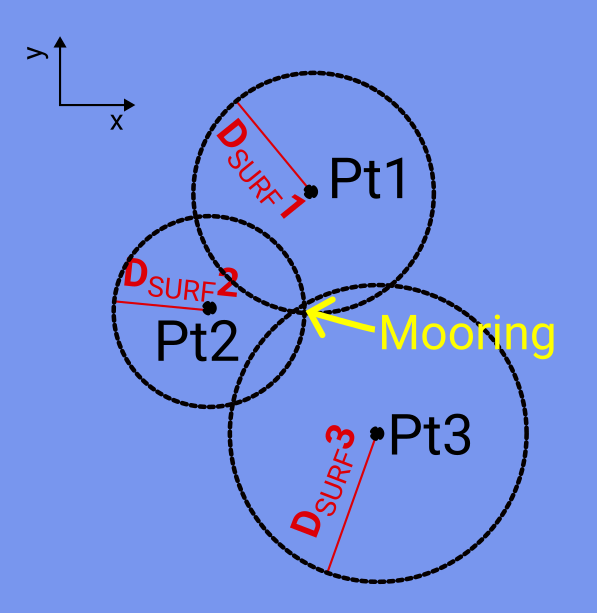
By measuring the distance from the ship on multiple locations to the acoustic release on bottom, we can use pythagoras to determine distances along the surface to the mooring position. If we measure close to a mooring that is located in deep ocean, small errors in measured distances can give large errors in the distance calculated along the surface.

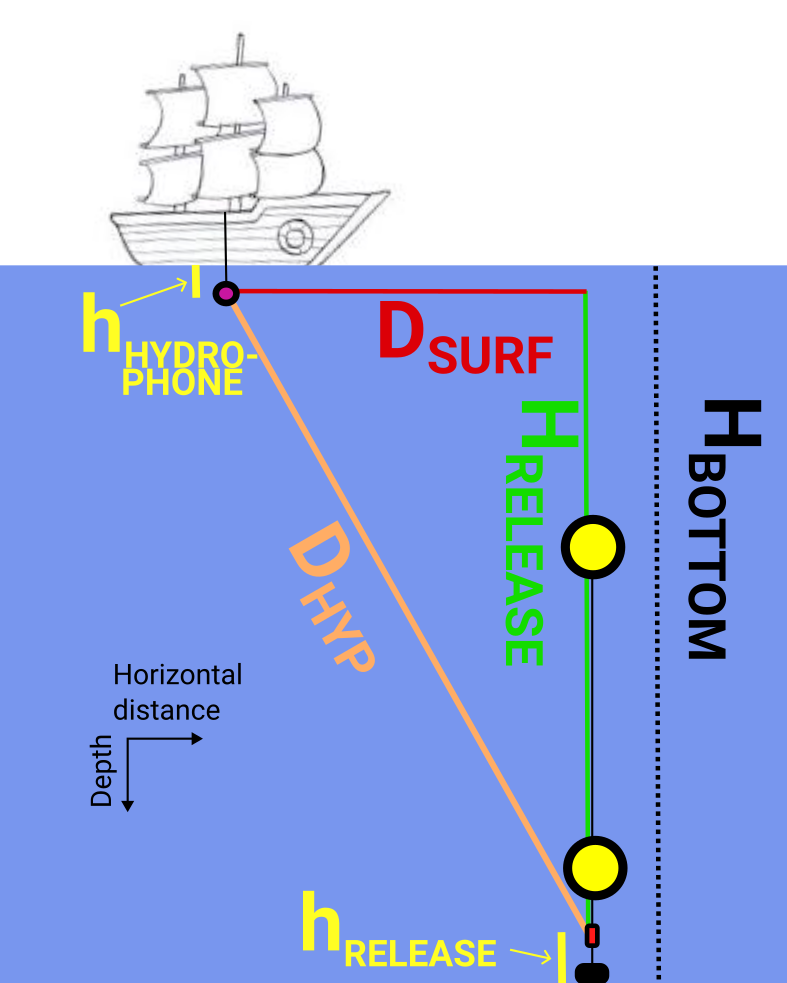
Errors in measured distance (hypothenuse in the triangle) to be aware of: An older instrument for release was used during this cruise, where the speed of sound in water cannot be adjusted. Normally the speed of sound is then set to 1500 m/s, while the echosounder on the ship was set to 1469 m/s. By correcting the measured distance by the factor 1469/1500 (about 2% reduction) we got a much better estimate of the location where mooring F11 was dropped.

Corrections in the depth estimate: The acoustic release that we ping is located 10m above the sea bottom, and the hydrophone is about 15 m below surface when making measurements, so we can subtract a total of 25 m from the depth estimate when using it for triangulation.

\[ D_{SURF}= \sqrt{\bigg(D_{HYP}\cdot\frac{c_{TRUE}}{c_{PROGRAMMED}}\bigg)^2 - \bigg(H_{BOTTOM}- h_{RELEASE}- h_{HYDROPHONE}\bigg)^2}\]

Where:

  • \(D_{HYP}\) is the travel distance of the return signal as estimated by the surface acoustic transducer unit.

  • \(c_{PROGRAMMED}\) is the acoustic sound speed programmed into the surface acoustic transducer unit.

  • \(c_{TRUE}\) is the best available estimate of he true sound speed

  • \(H_{BOTTOM}\) is the water depth at the mooring site.

  • \(h_{RELEASE}\) is the height of the acoustic release above the bottom.

  • \(h_{HYDROHPONE}\) is the depth of the hydrophone transducer below the sea surface.

Notes from the FS2024 cruise#

We pinged the mooring from at least three different locations around it, and got the captain on KPH to draw a circle on the map with a radius equal to the estimated distances to the mooring. If you have good estimates of the distances along the surface to the mooring, the intersection of three circles on the map should be enough to indicate where the mooring is located.

I calculated the distance by simply applying the Pythagorean theorem in Python:

Horizontal distance = np.sqrt((dist*1469/1500)**2 - (depth-25)**2)

Here, dist is the distance from the hydrophone (the hypotenuse of the triangle), 1469/1500 is a correction to the distance due to an assumed error in the speed of sound in water, depth is the water depth, and we subtract 25 m from the water depth to account for the approximately 10 m that the release is above the seafloor and the 15 m that the hydrophone is below the surface.

The values you need to input might be different, since you’re probably using a different ship and maybe a different hydrophone, but the principle is the same. If your moorings are in very deep water, be aware that the distance estimates are more uncertain.